Vault of Therayne

An easter egg and puzzle solution for Dungeon Siege 2 Broken World.

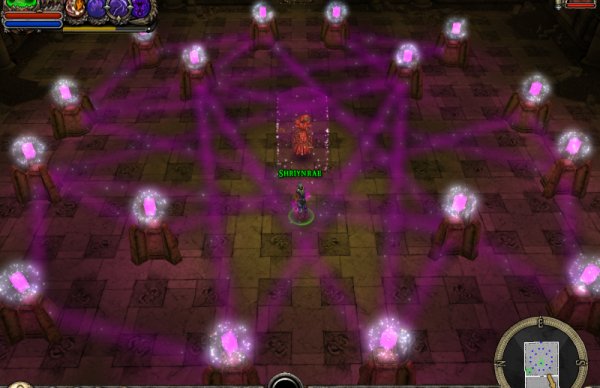
After doing the first two rooms of the Treasure Hunt quest, you can attempt two additional puzzles of the same type, but these are ridiculously hard. If you made the second one, you have no doubt noticed that these are much trickier than the general lightning reflection puzzle in the original DS2. The third is manageable with a good dose of trial and error - still more than expected for an otherwise mindless hack'n slash game - but the last one is almost impossible.

So I present a mathematical way to solve it. First three solutions are included for completeness, the method used is at the end.

R1: Square

Click each node once.

R2: Square + Square

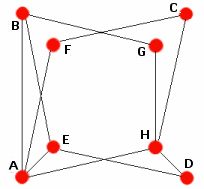
Click nodes $A,C,F,H$ once, in whatever order.

R3: Octagon + Square

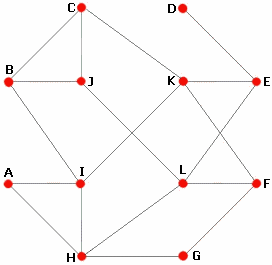
Found two solutions here; one from trial and error: $B,E,G,I,J,K,L$

While this came out of mathematica: $B,C,D,G,I,K,L$

R4: Dodecagon + Square

The one that necessitated math.

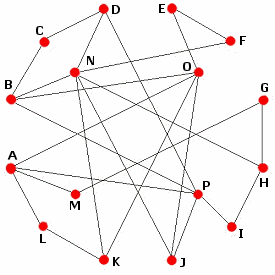
Derived solution: $B,E,F,G,I,J,K,N,O$

Developer solution: $B,C,D,E,G,K,P$

Pick one, and press each node once in any order.

Method

Every block must be inverted an odd number of times, and since inverting twice is the same as not doing anything, these operations are equivalent to addition mod 2.

Each row $j$ in matrix $\mathbf{V}$ represents which lights are inverted by $f(j)$. For instance: $f(A)$ inverts A, L, M, O, and P (as shown in the diagram), which is the first row in V.

V={{1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1},
  {0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1},
  {0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
  {0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1},
  {0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0},
  {0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0},
  {0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0},
  {0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0},
  {0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1},
  {0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1},
  {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0},
  {1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0},
  {1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0},
  {0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0},
  {1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0},
  {1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1}}

Solving the equation $\mathbf{Vx} = {1,1,....1} \mod{2}$ reveals how many times one must utilize $f(j)$ to invert every light source.

i={1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}

LinearSolve[V, i, Modulus -> 2]
Answer: {0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0}

in other words: $B,E,F,G,I,J,K,N,O$

This post was later found by one of the game developers who sent me their solution; $B,C,D,E,G,K,P$, and this yields all odds when taking the dot product with $V$.